ارمغان بوشهر

مقدمه

در پانزدهمین کنفرانس آموزش ریاضی ایران در بوشهر، سؤالی مطرح شد که چرا معمولاً، متغیر مستقل تابع‌های مثلثاتی را برحسب رادیان می‌نویسند و اگر مثلاً درجه به‌جای آن بگذارند، چه اشتباهی ممکن است رخ دهد. بحث مزبور، انگیزه‌ای برای نوشتن مقاله حاضر شد. با تابع سینوس آغاز می‌کنیم و موارد مشابه را به خواننده علاقمند، وا می‌گذاریم.

هر تابع y= f(x) را می‌توان جدولی دو ستونی انگاشت که در یک ستون، مقدارهای متغیر مستقل و در ستون دیگر، مقدارهای متغیر تابع را نظیر به نظیر نوشته باشند. بدیهی است که اگر دامنه تابع، یک مجموعه بی‌نهایت عضوی باشد، نوشتن همه مقدارها غیرممکن است و در محاسبه‌های رایانه‌ای، به نوشتن تعدادی متناهی بسنده می‌کنند. مثلاً در جدول سینوس‌ها، زاویه‌های 0 تا 90 درجه را به ترتیب، زیر هم، در یک ستون می‌نویسند و مقابل هر زاویه مقدار سینوس آن را در ستونی دیگر ثبت می‌کنند. در زمان‌های گذشته که رایانه نبود و یا اگر بود، استفاده از آن‌ها رایج نبود، سینوس هر زاویه دیگر را با تقریب و درون‌یابی حساب می‌کردند. در جدول سینوس‌های صفحه بعد، یک ستون هم برای مقدارهای زاویه (متغیر مستقل) بر حسب رادیان اضافه کرده‌ایم. بستگی به این که کدام یک از دو ستون «رادیان» یا «درجه» را به کار بگیریم یک تابع مثلثاتی خاص به دست می‌آوریم که از نظر هندسی هیچ فرقی با هم ندارند، ولی از نظر حسابان با هم متفاوتند.

تابع سینوسی

در جدول سینوس‌ها، از کنار هم گذاشتن ستون سمت چپ (رادیان) و ستون سمت راست (سینوس)، تابعی به دست می‌آید که آن را با دستور y= sin_r(x) نمایش می‌دهیم. همچنین با کنار هم گذاشتن ستون وسط (درجه) و ستون سمت راست (سینوس)، تابع دیگری به دست می‌آید که به صورت y=sin_d(x) نمایش می‌دهیم. همان‌طور که گفتیم اگر متغیر مستقل را زاویه هندسی بگیریم و از اندازه (عددی) زاویه چشم بپوشیم، تابعی با دامنه هندسی به دست می‌آید که آن را با نماد ساده y=sin x نمایش می‌دهیم.

در تابع مثلثاتی هندسی نباید از مقدار زاویه سخن گفت بلکه باید به شکل آن اشاره کرد؛ مثلاً می‌گوییم سینوس زاویه قائمه برابر با 1 می‌باشد، سینوس نصف قائمه برابر با  است، سینوس هر زاویه در مثلث متساوی‌الاضلاع برابر  است و غیره. اما وقتی که متغیر مستقل در مجموعه عددهای حقیقی قرار می‌گیرد دو تابع y =sinr(x) و y =sind(x) متفاوت هستند؛ برخی از مقدارهای این دو تابع را در زیر نوشته‌ایم تا تفاوت‌ها را مشاهده کنید:

گرچه سینوس‌های «رادیانی» و «درجه‌ای» دو تابع متفاوت تعریف می‌کنند ولی یک رابطه خطی ساده آن‌ها را به هم پیوند می‌زند؛ یعنی (*)  

توجه کنید که بسیاری از معادلات یا اتحادهای مثلثاتی بیش از آنکه جبری باشند، هندسی هستند و لذا به اندازه زاویه‌ها وابسته نیستند. مثلاً معادله زیر یا اتحاد بعد از آن ربطی به واحد اندازه‌گیری زاویه‌ها ندارند:

مشکل اساسی ما با تابع‌هایی از نوع زیر است:

که در آن عبارت x2 برای هر دو نوع کمیت عددی و هندسی قابل تعریف است و همانند همه چندجمله‌ای‌ها حساسیتی نسبت به واحد اندازه‌گیری نشان نمی‌دهد. لگاریتم گرچه برای شکل‌های هندسی بی‌معنی است ولی مانند چندجمله‌ای‌ها نسبت به واحد اندازه‌گیری بی‌تفاوت است. عبارت سینوس، نه تنها در حسابان بلکه در هندسه هم معنادار است؛ البته نسبت به انتخاب واحد اندازه‌گیری حساسیت نشان می‌دهد. اینجا است که باید تکلیفمان را با واحد اندازه‌گیری روشن کنیم.

از این پس ما هیچ نیازی به مطالعه تابع سینوس هندسی نداریم و لذا نماد آن را به تابع سینوس رادیانی اختصاص می‌دهیم؛ یعنی از این پس به ازای همه مقادیر حقیقی x، قرار می‌گذاریم sin_rx=sinx. حال ببینیم اگر سینوس رادیانی به سینوس درجه‌ای تبدیل گردد، معادله (**) چه تغییراتی می‌کند. توجه کنید که اگر  آنگاه، با فرض  ، 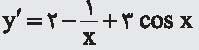 اما اگر سینوس را با سینوس درجه‌ای عوض کنیم، آنگاه بنا بر (*)،

و در نتیجه مشتق تابع به صورت زیر تغییر می‌کند:

همچنین دوره تناوب آن که بازه تقریبی 0 تا 28/6 بود اینک بازه 0 تا 360 می‌باشد.

اثرگذاری رادیان

در این بخش از مقاله، دقت می‌کنیم که چگونه واحد اندازه‌گیری زاویه، خود را در محاسبه حد و مشتق نمایان می‌سازد. تأثیر آن در شکل تابع سینوسی واضح است؛ کافی است که فقط طول هر نقطه از منحنی سینوس رادیانی را به اندازه  کشش دهیم تا منحنی نمایش تابع درجه‌ای حاصل شود. لذا با دانستن مشتق تابع سینوس رادیانی، مشتق تابع سینوس درجه‌ای به آسانی به دست می‌آید. می‌ماند ثابت کنیم که مشتق تابع سینوس رادیانی برابر با تابع کسینوس رادیانی است:

که البته از دستور معروف  بهره گرفته‌ایم. پس باید دید که چگونه واحد اندازه‌گیری زاویه در برهان این دستور اخیر خودنمایی می‌کند. در صفحه xOy، نقطه‌های (0,0)=O، (1,0)A=،  B=(cost, sint) و C=(1, tant) را در نظر بگیرید و ملاحظه کنید که     

توجه شود که این نامساوی‌ها وقتی برقرارند که زاویه مرکزی t بر حسب رادیان باشد. (اگر t برحسب درجه باشد، آنگاه    در نتیجه، حد مطلوب از حدگیری دو طرف نامساوی‌های زیر به دست می‌آید:

سخن پایانی

معلمان و استادان ریاضی ستمدیده‌ترین قشر جامعه ما هستند. زیرا علاوه بر کار سخت و دستمزد کم، باید جور تصمیمات برنامه‌ریزانی را بکشند که قوانین را در جهت منافع اقلیت‌های خاصی وضع می‌کنند. در تدوین کتاب‌های درسی، به آنان فرصت اظهار مشکلات نمی‌دهند و تا آن‌ها به گوش شنوائی برسند، موسم کنکورهای رسمی و غیررسمی که زندگی مدرسان و اولیاء و دانش‌آموزان را مختل کرده‌اند فرا می‌رسد و باید چیزی را که عقل سلیمشان نپذیرفته، شتاب‌زده به دانش‌آموزانشان تدریس کنند. علاوه بر غائله رادیان که در بخش‌های قبل به آن پرداختیم، مسئله‌های دیگری هم در میان معلمان شرکت‌کننده در همایش بوشهر زمزمه می‌شد. مثلاً شیر پاک خورده‌ای، میدان را از اغیار خالی دیده با تعویض تعریف استاندارد پیوستگی در کتاب‌های درسی، و قرار دادن شرایط کافی پیوستگی از چپ و راست به جای آن، تابع  را از نعمت پیوستگی در مبدأ محروم کرده است؛ استادان ریاضی با چشمان خیره و دهان باز متحیر بودند که چرا با تولید این همه کارشناس ریاضی بیکار در مملکت، نوگشایی و بسط دانشگاه‌های فرهنگیان در اهم دستور کار دولت قرار گرفته است؟ چرا در این بلوای کسر بودجه برای دانشگاه‌های مادر و چشم و چراغ کشور، گرفتن دانشجوهای حضوری را به برنامه‌های تعریف شده پیام نور اضافه کرده‌اند و حتی مجوز دوره‌های تحصیلات تکمیلی را به آن‌ها داده‌اند، ...

متولی ریاضیات کشور، قبل از هر کس، انجمن ریاضی ایران است که حدود نیم قرن پیش، بار سنگین آن را بر دوش گرفت و یک کول کشاند تا شورای مرکزی انجمن‌های دبیران ریاضی استان‌ها، شورای مرکزی خانه‌های ریاضیات و شاخه ریاضی فرهنگستان علوم جمهوری اسلامی ایران، به کمکش شتافتند. هر نوع تصمیم‌گیری در مورد ریاضیات کشور بدون توافق با انجمن مزبور، خیانت به علم و جوانان آینده کشور است.