رسم نیمساز یک زاویه بدون گوشه

مسئله: زاویه بدون گوشه‌ای موجود است، نیمساز آن را چطور می‌توان رسم نمود؟

حل مسئله

می‌توانیم اضلاع زاویه را امتداد دهیم و محل برخورد را به‌دست آوریم، سپس نیمساز زاویه به‌دست آمده را رسم کنیم. اما سؤال اینجاست که اگر بخواهیم از راه‌های دیگری به نیمساز زاویه بدون گوشه برسیم، چه باید بکنیم یا چه می‌توانیم بکنیم؟

روش اول:

برای پیدا کردن نیمساز زاویه‌ای که گوشه آن را نداریم، می‌توانیم از همرسی نیمسازهای زاویه‌های داخلی مثلث استفاده کنیم. بنابراین، باید با این زاویه یک مثلث درست کنیم. برای این کار، ابتدا یک خط متقاطع دلخواه چنان رسم می‌کنیم تا دو ضلع زاویه را در دو نقطه A و B قطع کند.

سپس نیمسازهای دو زاویه A و B را رسم کرده و نقطه همرسی آن‌ها را M می‌نامیم.

ولی با یک نقطه نمی‌توان نیمساز زاویه بی‌گوشه را پیدا کرد. از آنجایی که همه مثلث‌های ایجاد شده مشابه مثلث بالا که زاویه بدون گوشه در آن‌ها ثابت است، نقطه همرسی نیمسازهایشان روی نیمساز زاویه بدون گوشه قرار خواهد گرفت، پس کافی است که مثلث دیگری با رسم یک خط متقاطع دیگر مانند DC ایجاد کنیم. آن‌گاه نقطه همرسی نیمسازهای داخلی آن را به‌دست آورده و آن را N می‌نامیم.

با وصل کردن دو نقطه M و N ، نیمساز زاویه بدون گوشه به‌دست می‌آید.

روش دوم:

از دو ضلع زاویه بدون گوشه، به یک اندازه مثلاً x، به درون زاویه رفته و دو خط موازی آن اضلاع، رسم می‌کنیم.

سپس دو خط موازی دیگر نیز به همان فاصله و موازی دو خط رسم شده، رسم می‌کنیم.

چهارضلعی ایجاد شده از تقاطع این چهار خط موازی را ABCD می‌نامیم.

چون چهارضلعی ABCD حاصل تقاطع خطوط موازی است، بنابراین متوازی‌الاضلاع است. ابتدا ثابت می‌کنیم این چهارضلعی لوزی است. از دو رأس B و D بر خطوط موازی عمود کرده تا دو مثلث قائم‌الزاویه BCH و DCG به‌دست آید. این دو مثلث به حالت دو زاویه و ضلع بین (زض‌ز) همنهشت هستند (طول عمودها برابر است DG=BH ، زاویه قائمه  و متمم زاویه‌های روبه‌رو در متوازی‌الاضلاع . در نتیجه DC=BC است، پس چهارضلعی ABCD لوزی است.

اگر نیمساز زاویه‌های B و D را رسم کنیم، نیمساز زاویه بدون گوشه خواهد بود. در واقع زاویه D، همان انتقال یافته زاویه بدون گوشه روی نیمساز آن است.

روش سوم:

خط e را موازی با یکی از خطوط زاویه چنان رسم می‌کنیم تا خط دیگر را در نقطه A قطع کند. زاویه تشکیل شده طبق خطوط موازی و خط مورب، با زاویه بدون گوشه شده برابر است.

سپس نیمساز زاویه A را رسم می‌کنیم.

نقطه B را روی ضلع بالایی زاویه بدون گوشه فرض کرده و بر نیمساز Ax، عمود BC را وارد می‌کنیم.

در مثلث ABD، چون Ax نیمساز و عمود وارد بر ضلع BD است، بنابراین مثلث ABD متساوی‌الساقین است. از آنجایی که دو زاویه C و D طبق خطوط موازی و خط مورب مساوی هستند، دو زاویه B و C نیز باهم برابرند. پس مثلث ایجاد شده بین پاره‌خط BC و دو ضلع زاویه بدون گوشه، متساوی‌الساقین می‌باشد.

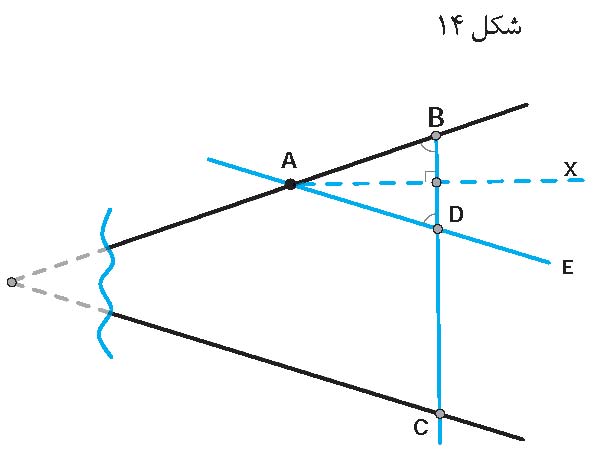
حال اگر عمودمنصف پاره‌خط BC را رسم کنیم، همان نیمساز زاویه بدون گوشه خواهد بود.

روش چهارم:

از یک نقطه دلخواه مانند M، دو خط عمود بر اضلاع زاویه رسم می‌کنیم.

نیمساز زاویه  را رسم می‌کنیم.

دو مثلث MHC و MGD بنابر برابری زاویه‌های  و  با هم متشابه هستند. پس می‌توان نتیجه گرفت دو زاویه C و D با هم برابرند. بنابراین، مثلث ایجاد شده از پاره‌خط CD و دو ضلع زاویه بدون گوشه (CED)، متساوی‌الساقین است.

یعنی برای رسم نیمساز زاویه بدون گوشه، کافی است عمودمنصف پاره‌خط CD را رسم کنیم.