چکیده
پژوهش حاضر با هدف ارتقای درک مفهومی دانش‌آموزان از مبحث تعیین علامت به کمک مثال‌های روزمره و دست‌سازه‌های ریاضی انجام شده است. بدین منظور، در مرحله نخست، به‌عنوان یک هدف پایه، چارچوبی برای آموزش تعیین علامت براساس مثال‌های روزمره و استفاده از دستسازه بر پایه کار میدانی طراحی و تولید شد. از بین ۵۸ دانش‌آموز پایه دهم یک مدرسه از شهرستان کازرون، به روش نمونه‌گیری ساده، دو گروه بیست نفره به‌عنوان گروه‌های آزمایش و کنترل انتخاب شدند. در این پژوهش «آموزش بر مبنای مثال‌های روزمره و دست‌سازه‌های ریاضی و آموزش به شیوه کتاب درسی» متغیر مستقل، و«ارتقای درک مفهومی دانش‌آموزان از مبحث تعیین علامت» به‌عنوان متغیرهای وابسته در نظر گرفته شدند. هر یک از گروه‌های آزمایش و کنترل طی جلسات تدریس این مبحث تحت‌تأثیر متغیرهای مستقل قرار گرفتند. برای تجزیه و تحلیل اطلاعات از «آزمون یومن- ویتنی» استفاده شد. نتایج تحقیق نشان داد که تفاوت معنی‌داری بین میزان یادگیری دانش‌آموزان دو گروه آزمایش و کنترل وجود دارد و یادگیری دانش‌آموزان گروه آزمایش به‌طور قابل ملاحظه‌ای از گروه کنترل بهتر بود.
مقدمه
گالیله می‌گوید: «جهان هستی همواره در برابر دیدگان حیرت‌زده انسان گسترده خواهد ماند و انسان هرگز نمی‌تواند آن را درک کند، مگر اینکه زبانی را که این جهان با آن نوشته و توضیح داده شده است، یاد بگیرد و حروف آن را بشناسد. این زبان چیزی جز ریاضیات نیست و این حروف جز مثلث، دایره و سایر اشکال هندسی چیز دیگری نیستند.»
«ریاضیات علم نظم است و موضوع آن یافتن، توصیف و درک نظمی است که در وضعیت‌های ظاهراً پیچیده نهفته است. ابزارهای اصولی این علم، مفاهیمی هستند که ما را قادر می‌سازند این نظم را توصیف کنیم.» ریاضیات تنها زبانی است که پدیده‌های طبیعی جهان هستی را به خوبی توضیح می‌دهد.
برقراری ارتباط بین مفاهیم ریاضی با سایر درس‌ها و علوم، و همچنین مسائل زندگی روزمره و کاربرد آنها (ارتباط بیرونی ریاضی) موجب می‌شود که دانش‌آموز در هر لحظه بتواند پاسخ این سؤال را که «این درس به چه درد می‌خورد؟» کسب کند.
هنگام آموزش ریاضی می‌توان ارتباط مفاهیم ریاضی را با زندگی، طبیعت و علوم مختلف بیان کرد. برای مثال می‌توان به استفاده از آمار در درک کدهای ژنتیکی [۹]، کاربردهای محاسبه سطح و حجم، و مثلثات در نقشه‌خوانی و نقشه‌برداری، کاربرد نماها و لگاریتم‌ها در محاسبه نرخ جمعیت، محاسبه نرخ بهره و نرخ رشد اقتصادی، و پیش‌بینی‌های اقتصادی که در برنامه‌ریزی‌ها نیاز است، اشاره کرد[۱۱]. از این قبیل مثال‌ها بسیار وجود دارند که می‌توان در آموزش ریاضی از آنها بهره گرفت.
در استانداردهای «انجمن ملی معلمان ریاضی» اشاره شده است[۲]: برنامه‌های آموزشی دانش‌آموزان از پیش‌دبستانی تا دبیرستان باید به‌گونه‌ای باشد که آنها بتوانند:
۱. ارتباط میان مفاهیم ریاضی را تشخیص دهند و به کار برند؟
۲. ارتباط مفاهیم ریاضی را دریابند و کل منسجمی را ایجاد کنند؟
۳. ریاضیات را در زمینه‌هایی غیر از ریاضیات تشخیص دهند و به کار برند.
هنگام تدریس ریاضیات می‌توان تمرین‌هایی ارائه کرد که ارتباط ریاضی با زندگی را نشان دهند. محدوده تمرین‌هایی که ارتباط با زندگی را نشان می‌دهند[۱]، عبارت‌اند از:
• قیاس‌های ساده (برای مثال، ارتباط دادن عددهای منفی با درجه حرارت زیر صفر)؛
• کلاسیک (برای مثال، «دو قطار ایستگاه را ترک می‌کنند اگر سرعت حرکت متفاوتی داشته باشند ...»)؛
• تجزیه و تحلیل داده‌های واقعی (برای مثال، پیدا کردن میانه و مد قد هم‌کلاسی‌ها)؛
• مباحث مربوط به ریاضیات در جامعه (برای مثال، سوء استفاده رسانه‌ها از آمار برای اینکه عموم را متقاعد سازند)؛
• «دست‌سازه‌ها»؛ نمودهایی از مفاهیم ریاضیات (برای مثال، مدل‌های جامدات منظم، تاس و ...)؛
• مدل‌سازی ریاضی پدیده‌های واقعی (برای مثال، نوشتن یک فرمول برای بیان درجه حرارت به‌عنوان تابعی از روز به سال).
مبانی نظری تحقیق
بعد از یادگیری یا یاددهی هر مسئله یا مطلب تئوری ریاضی، اولین سؤالی که به ذهن خطور می‌کند این است که «دانستن این موضوع چه فایده عملی می‌تواند برای ما داشته باشد؟» پاسخ‌های قانع‌کننده به این سؤال می‌تواند میزان انگیزه، توجه و احساس نیاز ما را برای یادگیری آن موضوع افزایش دهد و لذا میزان سرعت و عمق یادگیری را بالا ببرد. یادگیری عمیق می‌تواند شانس پیدا کردن رابطه‌های جدید بین متغیرهای موجود در طبیعت یا کشف یک فایده عملی تازه برای مطالب نظری را افزایش دهد.
با ارائه مثال‌های ساده عملی، می‌توان ارتباط ریاضی را با دنیای واقعی نشان داد. از طرف دیگر، بسیاری از دبیران ریاضی به خاطر ناآشنایی با ساخت و به کارگیری مناسب دست‌سازه‌های ریاضی در تدریس، کمتر از دست‌سازه‌ها استفاده می‌کنند. بسیاری از آنها با این تصور که تنها آزمایشگاه ریاضی، ذهن انسان است و باید دانش‌آموزان دبیرستانی را به سمت تفکر مجرد و انتزاعی سوق داد، از به کارگیری دست‌سازه‌ها و نمودارهای مناسب در طول تدریس خودداری می‌کنند.
هدف از به‌کارگیری دست‌سازه‌ها و نمودارها در تدریس، جایگزینی آنها به جای استدلال‌های ریاضی نیست، بلکه هدف بالا بردن سرعت و عمق یادگیری استدلال‌های مجرد ریاضی توسط دانش‌آموزان و تقویت قوه تخیل آن‌هاست. همچنین، استفاده از دست‌سازه‌ها نه تنها حجم توضیحات معلم برای برقراری ارتباط بهتر با دانش‌آموزان را کمتر می‌کند، بلکه به‌صورت علمی به این سؤال دانش‌آموزان پاسخ می‌دهد که: «نفر اولی که این قضیه یا مطلب ریاضی را ثابت کرد، از کجا به درستی آن پی برده است؟» به خصوص، این تصور نادرست را که «حل مسئله، درست فکر کردن و کشف حقایق، فقط مخصوص دانشمندان بزرگ است»، در دانش‌آموزان اصلاح می‌کند.
نقش دست‌سازه‌ها در تقویت شهود ریاضی دانش‌آموزان
۱. استفاده از شهود و تعبیر هندسی
یکی از روش‌هایی که می‌تواند درک مطالب ریاضی را برای دانش‌آموزان ساده‌تر و عمیق‌تر کند، استفاده از قوه شهود و تعابیر هندسی مطالب است.
۲. روش طراحی دست‌سازه‌های ریاضی برای تدریس
طراحی و ساخت دست‌سازه‌های مناسب ریاضی توسط معلم نیازمند موارد زیر است:
۱. آشنایی با تعابیر هندسی و توانایی ساخت تعابیر هندسی مجازی؛
۲. توانایی رسم دقیق اشکال هندسی و بعضی از خطوط خاص مربوط به آنها.
۳. تبحر و تسلط کامل بر محتوای آموزشی کتاب‌های درسی.
۴. آشنایی با طریقه نوشتن طرح درس مناسب برای حل مشکلات یادگیری دانش‌آموزان.
۵. آشنایی با علل عدم یادگیری دانش‌آموزان که مهم‌ترین آنها عبارت‌اند از:
• ضعیف بودن قوه تخیل دانش‌آموزان؛
• یاد نگرفتن پیش‌نیازها و فقیر بودن گنجینه لغات و اطلاعات دانش‌آموزان؛
• علاقه نداشتن دانش‌آموزان به درس ریاضی به سبب عدم احساس نیاز به یادگیری آن؛
• مشکل بودن درک ارتباط بین اجزای بعضی از مطالب ریاضی.
۳. چگونه از دست‌سازه‌ها هنگام تدریس استفاده کنیم؟
استفاده از دست‌سازه‌ها در تدریس می‌تواند به عمل فرضیه‌سازی و استدلال برای حل مسائل کمک کند. اما میزان موفقیت برای این عمل به نحوه استفاده و به‌کارگیری معلم از دست‌سازه‌ها و میزان علاقه، انگیزه و همکاری دانش‌آموزان در طول تدریس بستگی دارد. معلمی که دست‌سازه‌ای را می‌سازد و در نقطه آغازین تدریس، شروع به توضیح نحوه عملکرد دستسازه و بیان ارتباط بین هدف نهایی تدریس و دستسازه می‌کند، مجال فکر کردن و مشارکت را از دانش‌آموزان سلب می‌کند و ناخواسته از کارایی دستسازه می‌کاهد. همچنین، اگر دانش‌آموزان انگیزه و علاقه‌ای به یادگیری عمیق مطالب نداشته باشند، آن‌گاه برای پیشبرد اهداف تدریس و استفاده بهینه از قابلیت‌های دستسازه همکاری چندانی از خود نشان نمی‌دهند. به این ترتیب، معلم مجبور می‌شود مانند سابق مطالبش را فقط به‌صورت تئوری و در قالب سخنرانی بیان کند.
روش تحقیق
در این پژوهش، برای آگاهی از میزان تأثیر استفاده از دستسازه و شهود، در یکی از مدرسه‌های شهرستان کازرون، از بین ۵۸ دانش‌آموز پایه دهم، به روش نمونه‌گیری ساده، دو گروه بیست نفره به‌عنوان گروه آزمایش و کنترل انتخاب شدند. درگروه کنترل مبحث تعیین علامت با همان ساختار گفته‌شده در کتاب درسی و حل فعالیت‌ها و تمرین‌ها تدریس شد. اما در گروه آزمایش، به منظور ارتقای درک مفهومی دانش‌آموزان از مبحث تعیین علامت، چارچوبی برای آموزش این مبحث بر اساس دو بخش زیر ارائه شد:
• به کمک درک شهودی (استفاده از مثال‌های کاربردی و روزمره ـ استفاده از دست سازه)؛
• به کمک روابط جبری.
قبل از شروع تدریس، مثالی عینی و روزمره برای آشنایی دانش‌آموزان با موضوع مورد بحث مطرح کردیم و سپس به معرفی آن پرداختیم. (جدول ۱).
بعد از آن به کمک دستسازه، موارد متفاوت تعیین علامت چندجمله‌ای‌های درجه اول و دوم را با دانش‌آموزان بررسی کردیم و وابسته بودن علامت هر عبارت را به ضریب جمله با بزرگ‌ترین درجه عبارت نشان دادیم (تصویر ۱).
تصویر ۱
سپس مثال‌های متنوعی از تعیین علامت در زندگی روزمره ارائه شد که نمونه‌هایی از آنها در ادامه آورده شده‌اند. از آنها خواسته شد با توجه به مطالبی که یاد گرفته‌اند و مطالب ذکرشده، مثال‌های دیگری ذکر کنند. در نهایت روش‌های تعیین علامت عبارت‌های درجه اول و درجه دوم براساس روابط جبری، بیان و اثبات شدند.
مثال‌هایی برای تعیین علامت عبارت درجه اول
۱. تصویر ۲ میزان pH را نشان می‌دهد. اگر عدد ۷ باشد، حالت خنثی (مقدار صفر یا ریشه)، کمتر از ۷ حالت اسیدی و بیشتر از ۷ حالت قلیایی (مخالف حالت اسیدی) خواهیم داشت که در واقع شبیه تعیین علامت عبارت‌های درجه اول است که در دو طرف ریشه علامت‌ها مخالف هم هستند.
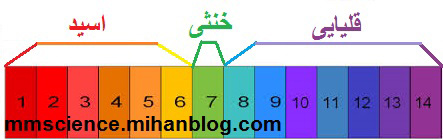تصویر ۲
۲. تغییرات دمای هوا نیز رفتاری مشابه تعیین علامت عبارت درجه اول دارد (تصویر ۳).
تصویر ۳
۳. نمودار ۱ نیز تلفات شبکه برق در کشورهای متفاوت را نشان می‌دهد که رفتاری مشابه تعیین علامت عبارت‌های درجه اول دارد.
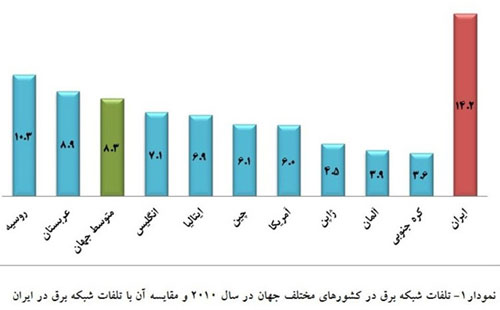نمودار ۱
۴. تابلوی تصویر ۴ را بارها در جاده مشاهده کرده‌ایم. این تابلو حاوی پیامی بازدارنده است. به عبارت دیگر، راننده باید حداکثر سرعت ۱۲۰ کیلومتر بر ساعت را در این مسیر رعایت کند. در غیر این صورت یک امتیاز منفی (جریمه) به وی تعلق می‌گیرد. بنابراین از این مثال می‌توان به‌عنوان یک عبارت درجه اول با ضریب پیشرو منفی استفاده کرد.
تصویر ۴
۵. کارنامه تحصیلی دانش‌آموزان یا کارنامه آزمون‌های زبان (تافل، تولیمو و ...)، نمونه دیگری برای درک مفهوم تعیین علامت عبارت درجه اول با ضریب جمله پیشرو مثبت است. حد نصاب نمره قبولی در این آزمون‌ها در واقع همان ریشه عبارت است. قبولی در هر آزمون، مجموعه جواب نامعادله محسوب می‌شود. (جدول ۲)
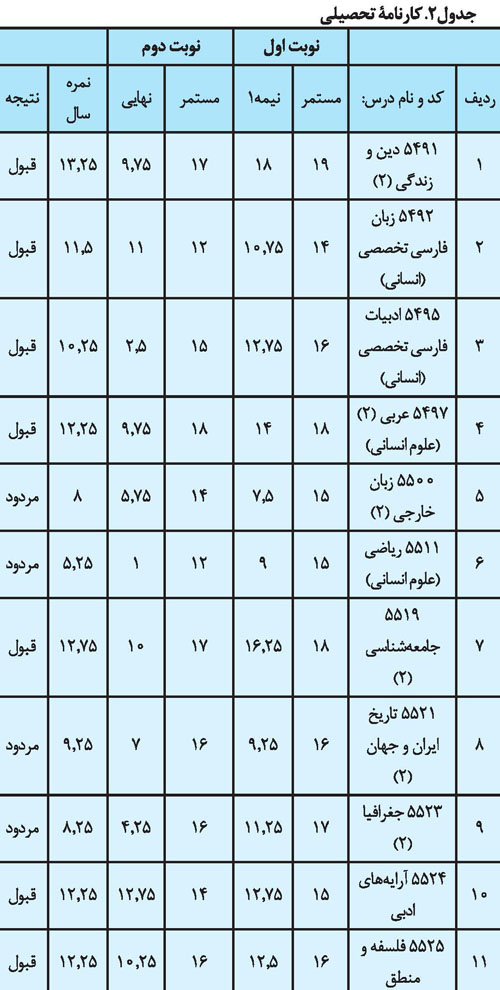جدول ۲
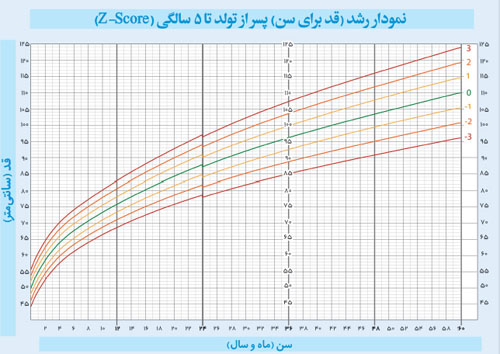
۶. نمودار رشد (قد برای سن) از تولد تا پنج سالگی را می‌توان به عنوان نمونه دیگری از تعیین علامت عبارت‌های درجه اول به کار برد. به این صورت که اگر منحنی رشد کودک زیر منحنی سبز رنگ قرار گیرد، رشد کودک کمتر از حالت استاندارد است و برعکس. (نمودار ۲)
نمودار ۲
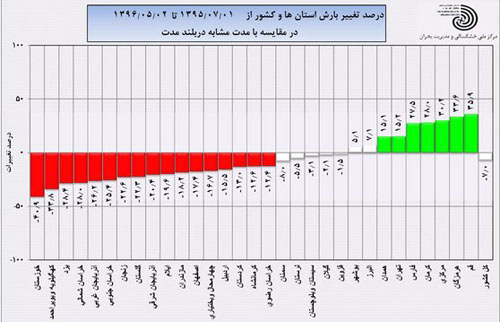
۷. درصد تغییرات بارش هر استان در مقایسه با مدت مشابه در بلندمدت، نمونه دیگری از جدول تعیین علامت عبارت‌های درجه اول است. این درصد برای هر استان ممکن است مثبت، صفر یا منفی باشد. (نمودار ۳)
نمودار ۳
۸. پرداخت مالیات از دیگر مواردی است که می‌توان از آن به‌عنوان تعیین علامت یک عبارت درجه اول استفاده کرد. مالیات حقوق سال ۱۳۹۸ تا سقف۰۰۰/۷۵۰/۲ تومان در ماه صفر است یعنی هر شخصی که ماهانه دو میلیون و هفتصد و پنجاه هزار تومان حق‌السعی دریافت می‌کند، از پرداخت حق دولت معاف خواهد شد. برای افرادی که دستمزد دریافتی آنها در سال ۱۳۹۸ بیش از ۰۰۰/۷۵۰/۲ تومان در ماه است، محاسبه مالیات حقوق سال ۱۳۹۸ مطابق با دستورالعمل‌هایی که از قبل مشخص شده، انجام می‌شود. (تصویر ۵)
تصویر ۵
۹. یکی از مثال‌های کاربردی در زمینه تعیین علامت عبارت‌های درجه اول با ضریب جمله پیشرو منفی، الگوی صحیح مصرف آب است. به این صورت که اگر مصرف روزانه هر فرد از حد استاندارد الگوی مصرف بهینه کمتر باشد، به‌صورت مثبت ارزیابی می‌شود و برعکس. (تصویر ۶)
تصویر ۶
عبارت‌های درجه ۲
الف) عبارت‌های درجه دوم شامل دو ریشه حقیقی
۱. نمودار ۴ مربوط به رشد جمعیت است. خط آبی‌رنگ نشان‌دهنده متوسط رشد جمعیت جهان است. همان‌طور که مشاهده می‌شود، در یک فاصله زمانی رشد جمعیت زیر خط آبی رنگ (علامت منفی) و در بقیه قسمت‌ها تقریباً بالای خط آبی (علامت مثبت) است و این همانند تعیین علامت یک عبارت درجه دوم است.
۲. همان‌طور که مشاهده می‌کنید، جدول مربوط به فشار خون مشابه جدول تعیین علامت عبارت‌های درجه دوم است. (جدول ۳)
جدول ۳
۳. در حالت طبیعی دمای درونی بدن ۵/۳۶ تا ۳۷ درجه است (مثبت) و خارج از این محدوده وضعیت طبیعی نیست (منفی) (جدول ۴).
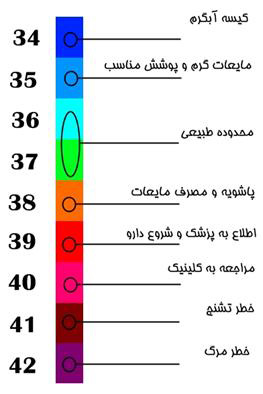جدول ۴
۴. با توجه به جدول ۵ مشاهده می‌شود که محدوده طبیعی کلسترول ۲۳۹-۲۰۰ است و خارج از این محدوده غیرطبیعی به شمار می‌رود.
جدول ۵
۵. محدودیت تردد در تهران، به صورتی است که از شنبه تا چهارشنبه (که یکی در میان خودرو‌های زوج و فرد را شامل می‌شود)، اجازه تردد از ساعت ۶:۳۰ تا ۱۹:۳۰ شب برای خودرو‌های غیر مجاز، ممنوع است. این ممنوعیت در روز‌های پنج‌شنبه تا ساعت ۱۳ است. در روز‌های تعطیل رسمی و جمعه‌ها محدودیتی وجود ندارد. این طرح، در عید نوروز، از ۲۹ اسفند تا ۱۳ فروردین اجرا نمی‌شود و تردد در هر محدوده‌ای بدون در نظر گرفتن پلاک آزاد است. در ماه مبارک رمضان طرح لغو نمی‌شود و فقط از ساعت ۱۹ به ۱۷ کاهش می‌یابد. با توجه به شرایط جوی، در نیمه دوم سال، یعنی از اول مهر تا پایان آذر ماه، دو ساعت کمتر می‌شود و از ساعت ۱۹ به ۱۷ انتقال می‌یابد. به دلیل آلودگی زیاد و برای داشتن هوای بهتر، در روز‌هایی که تحت‌عنوان «روز آلوده» شناخته می‌شوند، این طرح از ساعت ۶:۳۰ دقیقه صبح تا ساعت ۱۹ اجرا می‌شود. (تصویر ۷)
تصویر ۷
۶. میزان مصرف روزانه خوراکی‌ها و رژیم غذایی را با توجه به میزان مصرف تعداد واحد در گروه‌های متفاوت غذایی، از جمله غلات، میوه‌ها، سبزیجات، پروتئین، لبنیات و روغن و چربی‌ها، در تصویر ۸ مشاهده می‌کنید.
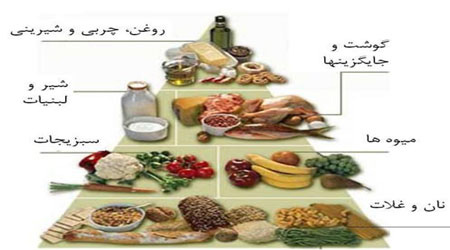تصویر ۸
۷. سیستم حلزونی گوش ما نسبت به فرکانس‌های متفاوت صوت پاسخ می‌دهد، اما اثر روانی آن برای ما زیر یا بم بودن صوت است. محدوده قابل شنیدن برای انسان ۲۰ تا ۲۰۰۰۰ هرتز است. در گوش ما مناطقی وجود دارند که صداهای محدوده شنوایی ما را تقویت و خارج از این محدوده را حذف می‌کنند. (نمودار ۴)
نمودار ۴
ب) عبارت‌های درجه دوم شامل یک ریشه حقیقی
مسواک زدن همواره برای سلامت دندان‌ها مفید است و از دوران کودکی توصیه می‌شود؛ چه قبل از بیرون آمدن دندان‌های دائمی و چه بعد از آن. (تصویر ۸)
تصویر ۸
ج) عبارت‌های درجه دوم فاقد ریشه حقیقی
۱. ورزش همواره در هر سنی برای سلامتی ضروری است. البته باید حرکات ورزشی متناسب با شرایط بدنی فرد باشد. انتخاب زمان مناسب برای ورزش در طول شبانه روز نیز بسیار مهم است. (تصویر ۹)
۲. مصرف سیگار همواره برای سلامتی بدن انسان مضر است. حتی با ترک سیگار اثرات مخرب آن بر بدن تا آخر عمر باقی می‌ماند. (تصویر ۱۰)
• مثال‌های بسیاری پیرامون ما وجود دارند که قابل مقایسه با تعیین علامت عبارت‌هاست. حتی اعمال و رفتار ما نیز همین گونه است. برای مثال، راست‌گویی همواره عملی پسندیده (مثبت) است و یا دروغ‌گویی همواره عملی ناپسند (منفی) است.
• ضرب‌المثل «ز گهواره تا گور دانش بجوی» نیز نمونه بارزی از تعیین علامت عبارت درجه دوم فاقد ریشه است.
یا «کم گوی و گزیده گوی چون دُر / تا ز اندک تو جهان شود پُر» نمونه‌ای از تعیین علامت عبارت درجه اول است.
یافته‌ها
برای تحلیل نمره‌های به‌دست‌آمده، از گروه کنترل(B) و آزمایش(A) که اطلاعات مربوط به آنها در جدول ۶ و ۷ توصیف شده است، از آزمون یومن- ویتنی به منظور بررسی تأثیر روش تدریس به کمک مثال‌های روزمره و دستسازه بر میزان یادگیری ریاضی دانش‌آموزان کلاس دهم استفاده شد. با توجه به آزمون انجام‌شده، به نظر می‌رسد از نظر میزان یادگیری بین گروه آزمایش و کنترل تفاوت معناداری وجود دارد.
۱. بیان معنی‌داری یا عدم معنی‌داری تفاوت میزان یادگیری بین دو گروه آزمایش و کنترل
در تفسیر نتایج «آزمون یومن- ویتنی»، برای اینکه پی ببریم آیا تفاوت میزان یادگیری بین گروه آزمایش و کنترل متفاوت است، باید از نتایج جدول۸ استفاده کنیم. با استناد به مقدار sig (۰۳۴/۰) که در سطح خطای کوچک‌تر از ۰۵/۰ معنی‌دار است، باید گفت که با اطمینان ۹۵ درصد به لحاظ آماری تفاوت میزان یادگیری بین گروه A و B معنی‌دار است. یعنی میزان یادگیری بین گروه A و B متفاوت است. این نتیجه دلالت بر تأیید فرض H۱ تحقیق دلالت دارد که مبنی است بر تفاوت میزان یادگیری بین گروه A و B و در مقابل رد فرض H۰ مبنی بر عدم تفاوت میزان یادگیری بین گروه A و B.
۲. بیان کیفیت تفاوت میزان یادگیری در بین دو گروه آزمایش و کنترل
در تفسیر نتایج آزمون یومن- ویتنی، علاوه بر تعیین تفاوت معنی‌داری تفاوت یا عدم تفاوت میزان یادگیری در دو گروه دانش‌آموزان A و B، می‌توانیم پی ببریم که میزان یادگیری در کدام یک از دو گروه بیشتر و در کدام یک کمتر است. برای رسیدن به این منظور، می‌توانیم از نتایج جدول۲ استفاده کنیم. طبق نتایج این جدول، میانگین میزان یادگیری بین گروه A (۸/۲۳) بیشتر از میزان یادگیری در گروه B (۹۳/۱۷) است. در نتیجه درگروه A که یادگیری ریاضی با استفاده از روش دستسازه و مثال‌های روزمره انجام شده، میزان یادگیری بیشتر از گروه B است.
نتیجه‌گیری و پیشنهاد
نتایج این پژوهش مشخص کرد که استفاده از مثال‌های کاربردی و شهودی در کنار مثال‌های ریاضی، باعث تقویت انگیزه و به دنبال آن، یادگیری مفاهیم ریاضی برای دانش‌آموزان می‌شود. به‌طور ویژه استفاده از این روش در مبحث تعیین علامت، تأثیر چشمگیری بر افزایش سطح یادگیری دانش‌آموزان (به‌خصوص دانش‌آموزان بی‌انگیزه) و ارتقای درک آنها از این مفهوم داشت. شایان ذکر است که با استفاده از این شیوه نباید از بیان روش‌های جبری و دقیق ریاضی غافل شد، زیرا در این صورت یادگیری دانش‌آموزان سطحی خواهد بود.
پیشنهاد می‌شود دبیران محترم در تدریس مفاهیم ریاضی، با به کارگیری شهود، سعی در تسهیل مفاهیم انتزاعی داشته باشند تا به این ترتیب همه دانش‌آموزان را در فرایند یادگیری با خود همگام و همراه سازند. همچنین مؤلفان کتاب‌های درسی در صورت امکان در تدوین کتاب‌های درسی از مثال‌های روزمره و کاربردی برای درک بهتر دانش‌آموزان بیشتر استفاده کنند.
منابع
1. J. Gainsburg, (2008). "Real-world connections in secondary mathematics teaching", Journal of Mathematics Teacher Education, 2008.
2. National Council of Teachers of Mathematics, (2010). Standards for School Mathematics: Connections, Retrieved October 18, 2010, from National Council of Teachers of Mathematics Web site: http://www.nctm.org, 2010.
۳. بیژن‌زاده، محمدحسن(۱۳۹۳). آموزش و یادگیری ریاضیات، انتشارات خردمندان. تهران.
۴. تیموری، قاسم (۱۳۸۸). کاربردهای ریاضی در زندگی روزمره. مؤسسه فرهنگی منادی تربیت. تهران.
۵. (۱۳۸۸). مقدمه‌ای بر روش تدریس هندسه دبیرستان. مؤسسه فرهنگی منادی تربیت. تهران.
۶. (۱۳۸۸). طراحی و ساخت دست‌سازه‌های جبری. مؤسسه فرهنگی منادی تربیت. تهران.
۷. (۱۳۸۱). مقدمه‌ای بر روش تدریس ریاضی. مؤسسه فرهنگی منادی تربیت. تهران.
۸. سیف، علی اکبر (۱۳۹۱). تغییر رفتار و رفتار درمانی: نظریه‌ها و روش‌ها، انتشارات فروزش. تهران.
۹. فقهی، حسین (۱۳۷۱)، ریاضیات از نوع سوم، نگرشی جدید به کاربرد ریاضیات درباره جهان و انسان. نوظهور. تهران.
۱۰. لطفی، مریم؛ شمس دیلمی، هاجر؛ اکبرشاهی، اعظم؛ علیجانی، زهرا(۱۳۸۲)، مجموعه مقالات منتخب پنجمین کنفرانس آموزش ریاضی ایران (تأثیر شگفتی‌ها و جنبه‌های کاربردی ریاضیات در آموزش). انتشارات عابد. تهران.
۱۱. ملک حسینی، عباس؛ صالحی، عین‌اله؛ سایه وند، خسرو(۱۳۸۵)، ریاضیات و کاربرد آن درجغرافیا. سرا. تهران.