مجموعه‌های متناهی، نامتناهی، شمارا و ناشمارا

قبل از هر چیز به تعریف مفهوم تناظر یک‌به‌یک نیاز داریم که این مفهوم را به این صورت بیان می‌کنیم:

تناظر یک‌به‌یک: اگر A و B دو مجموعه باشند و به ازای هر عضو از A یک عضو از B و به ازای هر عضو از B یک عضو از A وجود داشته باشد، می‌گوییم A و B تناظر یک‌به‌یک دارند و می‌نویسیم: A≈B.

برای مثال، اگر فرض کنیم:  A = {۱,۲,۳,۴,۵,۶} و B = {a,b,c,d,f} ، در این صورت واضح است که: A=B. این تناظر یک‌به‌یک را به شکل زیر ملاحظه می‌کنید:

همان‌طور که در تعریف دقت کردید، مفهوم تناظر یک‌به‌یک بین دو مجموعه A و B هیچ محدودیتی برای نامتناهی بودن این دو مجموعه ایجاد نمی‌کند و اگر این مفهوم را به دقت به‌کار ببریم، به سادگی و به‌صورت زیر می‌توان نشان داد که مجموعه عددهای طبیعی و مجموعه عددهای طبیعی زوج تناظر یک‌به‌یک دارند؛ یعنی: N≈۲N

  (کمی جلوتر همین تناظر یک‌به‌یک بین مجموعه‌های نامتناهی را به صورتی دقیق‌تر و با تعریف تابعی دوسویی، یعنی تابعی یک‌به‌یک و پوشا بین دو مجموعه، نشان خواهیم داد).

حال به سراغ بحث اصلی می‌رویم و با تعریف مجموعه‌های متناهی و نامتناهی آغاز می‌کنیم.

 

مجموعه‌های متناهی و نامتناهی
تعداد حرف‌های صدادار انگلیسی از تعداد حرف‌های انگلیسی کمتر است. زیرا مجموعه اول جزو مجموعه دوم است. آیا این اصل در مورد مجموعه‌هایی چون N و زیرمجموعه‌های آن نیز صادق است؟ آیا می‌توان گفت تعداد اعضای مجموعه عددهای طبیعی و زوج، از تعداد اعضای N کمتر است؟

برای پاسخ به این سؤال باید مفاهیم متناهی و نامتناهی را در مجموعه‌ها بررسی کنیم و برای آن تعریفی جامع و مانع ارائه دهیم.

قبل از بررسی دو مفهوم متناهی و نامتناهی، به دلیل وابستگی این دو مفهوم به مفهوم «تعداد اعضا»، ابتدا مفهوم تعداد اعضا را بررسی می‌کنیم.

در مورد مجموعه‌هایی مانند مجموعه دانش‌آموزان و مجموعه صندلی‌ها، راه مستقیمی که برای مقایسه تعداد اعضای این دو مجموعه وجود دارد، شمارش تعداد اعضای هر مجموعه و مقایسه عددهای حاصل است.

اما آیا از این طریق می‌توان تعداد نقاط دو قطعه خط یا تعداد عددهای طبیعی و عددهای طبیعی زوج را با هم مقایسه کرد؟

برای رهایی از این مشکل، استفاده از «روش کانتور» بهترین راه‌حل است و آن برقراری تناظر یک‌به‌یک بین دو مجموعه است.

اگر مجموعه A را مجموعه دانش‌آموزان خارج از کلاس و مجموعه B را مجموعه صندلی‌های داخل کلاس تصور کنیم و بخواهیم بین A و B تناظری یک‌به‌یک برقرار سازیم، سه حالت ممکن است رخ بدهد:

۱. حالتی که هیچ دانش‌آموزی خارج از کلاس نمانده باشد و هیچ صندلی خالی نیز در کلاس نباشد. در این حالت، بین دو مجموعه A و B تناظری یک‌به‌یک برقرار شده است که می‌گوییم تعداد اعضای A و B با هم برابرند (A و B هم‌عدد هستند).

۲. حالتی که همه صندلی‌ها اشغال شده باشند و تعدادی دانش‌آموز در خارج کلاس باقی مانده باشند. در اینجا تعداد اعضای A بیشتر از تعداد صندلی‌ها بوده است. در این حالت، B با زیرمجموعه‌ای از A هم‌عدد شده است و نیز A با هیچ زیرمجموعه‌ای از B هم‌عدد نیست.

۳. حالتی که همه دانش‌آموزان روی صندلی نشسته باشند، ولی بعضی از صندلی‌ها خالی مانده باشند. در این حالت می‌توان گفت: تعداد اعضای B بیشتر از تعداد اعضای A است.

حال می‌توان با استمداد از مفهوم تناظر یک‌به‌یک، مقایسه بین تعداد اعضای دو مجموعه مانند A و B را مستقل از مفهوم عدد به‌صورت این تعریف‌ها تعمیم داد:

تعریف ۱. دو مجموعه A و B را هم‌عدد می‌گوییم و می‌نویسیم: ، هرگاه تناظری یک‌به‌یک بین A و B برقرار باشد.

تعریف ۲. اگر مجموعه A با زیرمجموعه‌ای از B هم‌عدد باشد، ولی B با هیچ زیرمجموعه‌ای از A هم‌عدد نباشد، می‌گوییم A ضعیف‌تر از B است و می‌نویسیم: A<B .

 

قضیه ۱. رابطه هم‌عددی در مجموعه مجموعه‌ها یک رابطه هم‌ارزی است.

I) A≈A

II) A≈B = B≈A

III) A≈B و B≈C = A≈C

قضیه ۲ را که به قضیه «کانتور و برنشتاین» یا قضیه «هم‌ارزی» معروف است، می‌پذیریم.

قضیه ۲. اگر مجموعه A با زیرمجموعه‌ای از B و نیز مجموعه B با زیرمجموعه‌ای از A هم‌عدد باشند، آن‌گاه دو مجموعه A و B با یکدیگر هم‌عدد خواهند بود.

مسئله ۱. ثابت کنید مجموعه نقاط پاره‌خط AC و DE با یکدیگر هم‌عدد هستند.

 
اثبات. تناظری یک‌به‌یک بین مجموعه نقاط دو پاره‌خط AC و ST وجود دارد. پس AC با زیرمجموعه‌ای از DE هم‌عدد است و نیز بین مجموعه نقاط DE و MN تناظر یک‌به‌یک وجود دارد. پس DE با زیرمجموعه‌ای از AC هم‌عدد است. پس بنابر قضیه هم‌ارزی، AC و DE هم‌عددند.

 

تعریف ۳. به ازای عدد طبیعی K، مجموعه عددهای طبیعی کوچک‌تر یا مساوی با K را قطعه Kام از عددهای طبیعی می‌نامیم و با N_K نشان می‌دهیم:


مثال.

تعریف ۴. مجموعه A را متناهی می‌نامیم، هرگاه تهی باشد یا با قطعه‌ای مانند NK از عددهای طبیعی هم‌عدد باشد. اگر A=Ø باشد، می‌گوییم تعداد اعضای A صفر است و اگر A≈N_K باشد، تعدادی اعضای A را (که عددی منحصربه‌فرد است) K می‌نامیم و می‌نویسیم: n(A)=K.
درواقع وقتی: A≈NK، بنابر مطالب گفته شده، بین A و NK تناظری یک‌به‌یک برقرار می‌شود و این به نوعی شمارش اعضای A توسط NK محسوب می‌شود.

 

 
مجموعه‌های متناهی ویژگی‌هایی دارند که آن‌ها را از مجموعه‌های نامتناهی جدا می‌کنند. مهم‌ترین آن‌ها عبارت‌اند از:

قضیه ۳. هر زیرمجموعه یک مجموعه متناهی، متناهی است و اگر A مجموعه‌ای متناهی باشد و: ، آن‌گاه:  0≤n(B)≤n(A

قضیه ۴. هیچ مجموعه متناهی نمی‌تواند با یک زیرمجموعه  محض ِخود (زیرمجموعه محض یاسره A مجموعه‌ای است چون B که BA و ) هم‌عدد باشد.

قضیه ۵. اگر A و B مجموعه‌هایی متناهی باشند، در این صورت:

I)  و  و (A-B) متناهی هستند.

II)

III)

 
حال این موضوع پیش می‌آید که مجموعه‌ای چون N با هیچ قطعه‌ای از N، یعنی با هیچ قطعه‌ای از خودش هم‌عدد نیست. پس متناهی نیست. به چنین مجموعه‌هایی چه می‌توان گفت؟ درست است این مجموعه‌ها که متناهی نیستند، نامتناهی نامیده می‌شوند، یعنی در حالت کلی:

تعریف ۵. مجموعه A را نامتناهی می‌نامیم، هرگاه متناهی نباشد. به عبارت دیگر، مجموعه A نامتناهی است، هرگاه تهی نباشد و با هیچ قطعه‌ای از عددهای طبیعی هم‌عدد نباشد.

مجموعه‌های نامتناهی نیز ویژگی‌های خاص خود را دارند که مهم‌ترین آن‌ها عبارت‌اند از:

قضیه ۶. هر مجموعه که زیرمجموعه‌ای نامتناهی داشته باشد، نامتناهی است.
 
قضیه ۷. هر مجموعه که با یک زیرمجموعه حقیقی خود هم‌عدد باشد، نامتناهی است.

قضیه ۸. مجموعه عددهای طبیعی نامتناهی است (کاربرد قضیه ۷، زیرا N با ۲N تناظر یک‌به‌یک دارد).

 
قضیه ۹. هر مجموعه که با یک مجموعه نامتناهی هم‌عدد باشد، نامتناهی است.

نتیجه: Z نامتناهی است.

 
(f تناظری یک‌به‌یک یا تابعی دوسویی است).
سرانجام به بحث بسیار مهم و شاید تا حدی چالش‌برانگیز می‌رسیم به نام مفهوم شمارایی و ناشمارایی!
چه مجموعه‌هایی شمارا یا شمارش‌پذیرند؟ آیا مفهوم شمارش‌پذیری و مفهوم متناهی در مجموعه‌ها معادل یکدیگرند؟ برای پاسخ به این سؤال‌ها باید تعریف مجموعه‌های شمارا و ناشمارا به درستی تبیین شود.

 
تعریف ۶. مجموعه A را شمارا یا شمارش‌پذیر می‌نامیم، هرگاه با N هم‌عدد باشد و اگر مجموعه‌ای متناهی یا شمارا باشد، آن را حداکثر شمارا می‌نامیم.

با توجه به تعریف ۶ می‌توان گفت:
۱. مجموعه‌های شمارا نامتناهی هستند (زیرا با N هم‌عدد هستند).

۲. هر مجموعه متناهی حداکثر شماراست.

۳. اعضای مجموعه‌های شمارا را می‌توان توسط N برچسب‌گذاری کرد. درواقع N مجموعه‌ای برچسب‌گذار است، همان‌طور که اگر A مجموعه‌ای متناهی باشد و: n(A)=K، مجموعه A را می‌توان توسط NK برچسب‌گذاری کرد.

۴. مجموعه‌های شمارا دو به دو هم‌عدد هستند.

۵. هریک از مجموعه‌های N و ۲N (عددهای طبیعی زوج) و Text Box: ۲N+۱، Z و W شمارا هستند.

۶. مجموعه N×N شماراست.


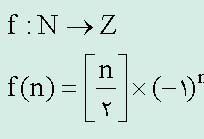
(به‌عنوان تمرین ثابت کنید این تابع دوسویی است).
۷. مجموعه Z (عددهای صحیح) شماراست.

(ثابت می‌شود که f تابعی دوسویی است و

 

همان‌طور که مشاهده می‌کنید، عددهای صحیح و مثبت توسط تأثیر f روی عددهای طبیعی زوج و بقیه توسط عددهای طبیعی فرد تولید می‌شوند).
 

 

قضیه‌های مربوط به مجموعه‌های شمارا
قضیه ۱۰. هر مجموعه نامتناهی، زیرمجموعه‌ای شمارا دارد.
اثبات: فرض کنیم A مجموعه‌ای نامتناهی باشد. عضو دلخواهی از A انتخاب می‌کنیم و آن را a۱ می‌نامیم. چون A نامتناهی است، پس A-{a۱} تهی نیست. عضو دلخواهی از A-{a۱} انتخاب می‌کنیم و آن را a۲ می‌نامیم. پس: a۱a۲. به همین ترتیب، به ازای عدد طبیعی n اعضای a۱، a۲ و ... و an را به طریق فوق که همگی دو به دو متمایز هستند، انتخاب می‌کنیم و از مجموعه A-{a۱,...,an} نیز عضو دلخواه an+۱ را. در نهایت مجموعه B={a۱,a۲,...,an,....} را که مجموعه‌ای شمارا و زیرمجموعه A است، می‌سازیم.

قضیه ۱۱. هر زیرمجموعه یک مجموعه شمارا، حداکثر شماراست.
اثبات: فرض کنیم A مجموعه‌ای شمارا باشد و: ، اگر E متناهی باشد که حکم ثابت است، و اگر E متناهی نباشد، بنابر قضیه قبل، زیرمجموعه‌ای شمارا چون E۱ دارد و چون A شماراست، پس: E۱≈A. از طرف دیگر داریم:  و E≈E. پس A زیرمجموعه‌ای هم‌عدد با E و E نیز زیرمجموعه‌ای هم‌عدد با A دارد. پس بنابر قضیه هم‌ارزی داریم:  و بنابراین E شماراست.

قضیه ۱۲. اگر A مجموعه‌ای شمارا و B مجموعه‌ای حداکثر شمارا و ناتهی باشد، مجموعه A×B شماراست.

 
در اثبات فوق، از قضیه ۱۳ که آن را بدون اثبات می‌پذیریم، استفاده شده است:


قضیه ۱۳. اگر E مجموعه‌ای ناشمارا باشد و A زیرمجموعه‌ای حداکثر شمارا را از E باشد، آن‌گاه:
E-A≈E .

 

قضیه ۱۴. هر مجموعه نامتناهی حداقل با یک زیرمجموعه حقیقی خود هم‌عدد است. اگر A نامتناهی باشد و B زیرمجموعه‌ای متناهی و ناتهی از A باشد، واضح است که (A-B) یک زیرمجموعه حقیقی A است و بنابر قضیه ۱۳ داریم: A-B≈A .

شاید جالب‌ترین نتیجه‌ای که بتوان از مطالب گفته شده گرفت، شمارش‌پذیر بودنِ مجموعه عددهای گویا، یعنی Q باشد که اگر فرض کنیم:

واضح است که با فرض Text Box: (m,n)=۱ (m و n نسبت به هم اول باشند)، هر  را به شکل منحصربه‌فردی می‌توان به‌صورت زوج مرتب (m,n) نمایش داد. در این حالت و با توجه به تعریف ضرب دکارتی می‌توان نوشت:

بنابراین ملاحظه می‌کنید که: Q≈Z×N و چون (قبلاً ثابت شد که Z×Z شماراست)، Z×N شماراست، پس Q نیز شماراست و نیز می‌توان نتیجه گرفت که (R-Q)، یعنی مجموعه عددهای گنگ، مجموعه‌ای ناشماراست.

قضیه ۵ مجموعه همه عددهای گویا شمارا است.

اثبات: دنباله‌ای از عددهای گویا را به‌صورت زیر می‌نویسیم:


هر کسر ، که p و q عددهای صحیح باشند و داشته باشیم: q>۰، نمایش یک عدد گویاست. اگر در فهرست بالا یا آنچه توسط فلش‌ها در شکل رسم شده‌اند، این دنباله به دسته‌هایی تقسیم شده که در هر دسته |p|+q ثابت است. بنابراین به ازای همه nها، دسته‌ها براساس |p|+q=n مرتب شده‌اند. به ازای n=۱,۲,۳,... یک دنباله نامتناهی به دست می‌آید و به این ترتیب تمام عددهای گویا شمرده می‌شوند.