اشاره
در این مقاله، ابتدا رویکرد آموزش ریاضی واقعیتمدار معرفی میشود و ارتباط آن با حوزه مدلسازی و کاربردها در آموزش ریاضی بیان میشود. در ادامه، با توجه به اینکه در «سند برنامه درسی ملی»، به کاربردهای ریاضی در دنیای واقعی اشاره شده، راهبردهایی برای استفاده از رویکرد آموزش ریاضی واقعیتمدار در کلاسهای درس ریاضی در سه بخش، ارائه شده است.
مقدمه
براساس ادبیات پژوهشی، رویکرد آموزش ریاضی «واقعیتمدار»1 بهعنوان واکنش هلندیها به دوران ریاضی جدید یا «ریاضی مدرن»2 شناسایی شده است. رویکرد آموزش ریاضی واقعیتمدار به رهبری هانس فرودنتال3، آموزشگر ریاضی هلندی، شروع شد و به گفته پنهیوزن4 (2001) این نهضت همچنان ادامه دارد. ایده اصلی در آموزش ریاضی واقعیتمدار این است که به دانشآموزان فرصت دهیم که ریاضی را تحت راهنمایی معلم خود، دوباره و توسط خودشان بسازند. در واقع، دانش رسمی ریاضی میتواند به وسیله دانش غیررسمی و عقل سلیم دانشآموزان توسعه یابد [Treffers, 1991]. این یعنی به وسیله انجام برخی فعالیتها، شامل حل مسائل زمینهمدار که برای دانشآموزان قابل درک هستند، آنها میتوانند از دانش غیررسمی خودشان برای خلق دوباره ریاضی استفاده کنند.
به عقیده فرودنتال (1991)، فعالیتهای ریاضی در آموزش ریاضی واقعیتمدار، هم میتوانند در دنیای واقعی مطرح شوند که باید براساس الگوهای ریاضی سازماندهی شود، و هم میتوانند در دنیای ریاضی مطرح شوند که باید براساس ایدههای جدید سازماندهی شوند تا بهتر فهمیده شوند.
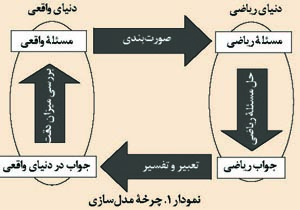
پژوهشگران آموزش ریاضی که در حوزه مدلسازی و کاربردها فعالیت میکنند، آموزش ریاضی واقعیتمدار را جزو پیشینه حوزه مدلسازی و کاربردها در آموزش ریاضی شناسایی کردهاند. منظور از مدلسازی در آموزش ریاضی چرخه نمودار 1 است که در آن، فرایند مدلسازی با یک مسئله که در موقعیت دنیای واقعی قرار دارد، شروع میشود. سپس با صورتبندی مسئله دنیای واقعی و تبدیل آن به یک مسئله ریاضی دنبال میشود. در ادامه، این مسئله ریاضی در دنیای ریاضی حل میشود و در نهایت، جوابی که در دنیای ریاضی به دست آمده است، باید به دنیای واقعی برده شود تا با زمینه واقعی مسئله متناسب شود [Verschaffel, 2002]. در اینجا ممکن است جواب دنیای ریاضی به تفسیر نیاز داشته باشد.
در سند برنامه درسی ملی جمهوری اسلامی ایران، یکی از هدفهای آموزش ریاضی، «توانایی بهکارگیری ریاضی در حل مسائل روزمره» عنوان شده است (دبیرخانه شورای عالی آموزشوپرورش، 1391). همچنین، در بخش دیگری از سند برنامه درسی آمده است که ریاضیات از نظر ماهیت، علمی مجرد است، ولی بستر رشد و توسعه آن، مشاهده، توصیف و تجزیه و تحلیل محیط پیرامونی است. در ریاضیات مدرسهای، فعالیت آموزشی باید برخاسته از ریاضیات محیط پیرامونی باشد. همه اینها نشان میدهند که کاربردی بودن ریاضی، جزو هدفهای اساسی نظام آموزشی ایران بوده و در اسناد بالادستی نظام آموزشی به آنها اشاره شده است.
مرور ادبیات پژوهشی به زبان فارسی نشان میدهد که چندین مقاله با تمرکز روی آموزش ریاضی واقعیتمدار نوشته شدهاند که از آن جمله میتوان به مقاله رفیعپور (1393 ب)، غلام آزاد (1393)، و ساویزی (1395) اشاره کرد. همچنین، تاکنون چندین پایاننامه کارشناسی ارشد آموزش ریاضی با محوریت رویکرد آموزش ریاضی واقعیتمدار انجام شدهاند که از طریق «پایگاه ایرانداک» قابل دسترسی هستند.
در مقاله حاضر، سه راهبرد مختلف برای استفاده از رویکرد آموزش ریاضی واقعیتمدار در کلاسهای درس ریاضی ارائه شده است. این راهبردها حاصل تجربیات نویسنده مقاله در پژوهشهای گوناگون و برگزاری کارگاههای آموزشی در حوزه مدلسازی و کاربردهاست.
راهبرد اول: محیط اطراف خود را با دقت مشاهده کنید.
توصیه کاربردی اول مبتنی بر ادبیات پژوهشی حوزه مدلسازی و کاربرد در آموزش ریاضی است. السینا (2007)، آموزشگر ریاضی اسپانیایی، در مقاله خود این ایده را مطرح میکند که در کلاس درس، کمتر از گچ و تخته استفاده کنیم و بیشتر از پدیدههای محیط زندگی خود برای طرح مسائل ریاضی بهره بگیریم. برای این کار، کافی است ابتدا دور و بر خود را خوب مشاهده کنیم و از اطلاعات منتشر شده در رسانهها که در دسترس هستند، به خوبی استفاده کنیم.
نویسنده مقاله حاضر از این رویکرد بارها برای طراحی مسائل متفاوت مدلسازی که برآمده از دنیای واقعی هستند، استفاده کرده است. بازخورد حاصل از اجرای این دست فعالیتها در کارگاههای مدلسازی، نشان میدهد که شرکتکنندگان در کارگاههای مدلسازی از حل اینگونه مسائل دنیای واقعی حس خوبی دارند.
برای مثال، شرایطی را در نظر بگیرید که شخصی با بودجه محدود قصد دارد یک گوشی هوشمند بخرد. مسئله این است که معیارهایی تدوین کنید و براساس این معیارها، راهنماییهایی به این شخص ارائه کنید تا او را در خرید گوشی هوشمند دلخواه یاری دهید. حتی میتوان چارچوب مسئله را مشخصتر کرد. مثلاً با بودجهای در حدود پنج میلیون تومان، فهرستی از گوشیهای هوشمند و ویژگیهای آنها را در اختیار دانشآموزان قرار دهید و از آنها بخواهید، یکی از این گوشیهای هوشمند را انتخاب کنند. این انتخاب باید براساس معیارهای متفاوت وزندهی به هر یک از معیارها، انجام شود. مثلاً ظرفیت باتری، کیفیت عکس، قدرت پردازنده و ... میتوانند از جمله معیارهایی باشند که در انتخاب بهترین گوشی هوشمند تأثیر بگذارند.
مشابه این مسئله را میتوان به سادگی برای سایر موقعیتها هم گسترش داد. مثلاً برای خرید بهترین «لپتاپ» با بودجه مشخص، یا خرید بهترین خودرو با بودجه محدود، یا انتخاب بهترین اپراتور تلفن همراه براساس عادتهای مکالمه افراد متفاوت، میتوان روند مشابهی را در نظر گرفت. گزارش اجرای نمونههایی از این دست فعالیتها، چاپ شده و در دسترس است. برای مثال، مقالههای احمدی و رفیعپور (1392 و 1393) در مورد انتخاب اپراتور تلفن همراه را ببینید.
راهبرد دوم: در مسائل کتابهای درسی تغییر کوچکی ایجاد کنید.
نتایج تحلیل محتوای کتابهای درسی ریاضی مدرسهای با استفاده از چارچوبهای نظری مختلف (برای مثال، رفیعپور، 1391 و خانی و رفیعپور، 1394) نشان میدهد که درصد کمی از مسائل کتابهای درسی ریاضی مدرسهای در حوزه مدلسازی و کاربرد قرار دارند. اما میتوان با ایجاد تغییرات کوچک در صورت مسائل، آنها را به مسائل کاربردی چالشی تبدیل کرد. بنابراین توصیه کاربردی دوم این است که با ایجاد تغییرات کوچک در مسائل موجود، آنها را به موقعیتهای دنیای واقعی مرتبط کنیم. مثلاً با درج اطلاعات بیشتر یا کمتر در صورت مسئله، آنها را چالشبرانگیز کنیم. برای ایجاد مسئله جدید از روی مسئله کتاب درسی، رهنمودهای مختلفی وجود دارند که در مقاله جداگانهای با جزئیات بیشتر به آن پرداخته خواهد شد.
البته لازم به ذکر است، مثالهایی از مسائل کلامی تفسیری (مسائلی که پاسخ نهایی آنها نیازمند تفسیر و مقابله با موقعیت مسئله است و نمونهای از آن در مقاله رفیعپور (1393، الف) آمده است)، در کتابهای درسی ریاضی مدرسهای قابل مشاهده است. اما از آنجا که فقط در موقعیتهای محدودی از مسائل کلامی تفسیری استفاده شده است، نمیتوان از دانشآموزان انتظار داشت در مواجهه با مسائل دنیای واقعی، عملکرد مطلوبی از خود به نمایش بگذارند. مثلاً مسائل مطرح شده در صفحه 174 کتاب درسی ریاضی اول دبستان، مسائل کلامی تفسیری هستند (تصویر 1). اما چون این مسائل در صفحههای پایانی کتاب درسی مطرح شدهاند و در سایر پایهها، مثالهای مشابه این مسائل دیده نمیشوند، خیلی اثرگذار نخواهند بود. لازم است مسائلی از این دست در سراسر مطالب کتاب درسی ریاضی و کلاسهای درس ریاضی مطرح شوند.

راهبرد سوم: از روشهای متفاوت برای طرح مسئله استفاده کنید.
یکی دیگر از راهبردهای مفید که برای طرح مسائل زمینهمدار دنیای واقعی، کارآمد است، استفاده از موقعیتهای متفاوت برای طرح مسئله ریاضی است. به گفته استویانوا و الرتون (1996)، طرح مسئله میتواند بهصورت آزاد، نیمهساختاری یا ساختاری باشد
• طرح مسئله در موقعیت آزاد: در این موقعیت فرد باید طبق تجربیات قبلی خود مسئله طرح کند. برای مثال، میتوان از دانشآموزان خواست برای دوست خود یک مسئله ریاضی طراحی کنند.
• طرح مسئله در موقعیت نیمه ساختار یافته: در این موقعیت باید برای شرایط داده شده، مسئله طرح کنند. مثلاً برای عبارت 5i+3i یک مسئله طرح کنید.
• طرح مسئله در موقعیت ساختاریافته: در این موقعیت باید بر پایه مسئلهای مشخص، مسائل دیگری طرح شوند. برای مثال، میتوان از دانشآموزان خواست براساس سؤال زیر، یک سؤال جدید طراحی کنند:
• چه تعداد پلاک خودرو با شکل کلی زیر میتوان برای شهر تهران صادر کرد؟
سخن پایانی
در این مقاله تلاش شد براساس ادبیات پژوهشی و تجربیات نگارنده در حوزه مدلسازی و کاربردها، سه راهبرد برای طراحی مسائل براساس رویکرد آموزش ریاضی واقعیتمدار، ارائه شود. این سه رویکرد شامل توجه بیشتر به محیط پیرامونی، تغییر مسائل کتابهای درسی ریاضی و استفاده از موقعیتهای طرح مسئله بود. استفاده از رویکرد آموزش ریاضی واقعیتمدار، بهطور مشخص میتواند در آموزش ریاضی در دوره همهگیری کرونا، مؤثر باشد. بهخصوص اگر با استفاده از دادههای منتشر شده در رسانهها درباره کرونا، یک مسئله ریاضی طراحی شود، آنگاه دانشآموزان با مسئله بهتر ارتباط میگیرند و برای حل آن تلاش بیشتری خواهند کرد.
پینوشتها
1. Realistic Mathematics Education
2. Modern Mathematics
3. Freudenthal
4. Panhuizen
منابع
1. احمدی، ح. و رفیعپور، ابوالفضل (1393). «انتخاب اپراتور تلفن همراه: یک مسئله مدلسازی ریاضی». مجله رشد آموزش ریاضی. شماره 116.
2. ــــــ (1392). «ریاضیات و تلفن همراه». مجله رشد آموزش ریاضی، شماره 112.
3. خانی، ن و رفیعپور، ابوالفضل (1394). «تحلیل محتوای کتابهای ریاضی جدیدالتألیف دوره ابتدایی براساس رویکرد مدلسازی». چاپ شده در مجموعه مقالات هفتمین همایش ملی آموزش. تهران.
4. دبیرخانه تولید برنامه درسی (1391). برنامه درسی ملی جمهوری اسلامی ایران: نگاشت نهایی. سازمان پژوهش و برنامهریزی آموزشی. تهران.
5. رفیعپور، الف (1391). «تحلیل محتوای مسائل کتاب حسابان براساس رویکرد مدلسازی». فصلنامه مطالعات برنامه درسی ایران. سال ششم. شماره 24.
6. رفیعپور، ابوالفضل (1393 الف). «مدلسازی و کاربردها: گزارش یک پژوهش». دو فصلنامه نظریه و عمل در برنامه درسی. سال دوم. شماره سوم. دانشگاه خوارزمی با همکاری انجمن برنامه درسی ایران.
7. رفیعپور، ابوالفضل (1393 ب). «واکنشهای پس از جنبش ریاضی جدید». مجله فرهنگ و اندیشه ریاضی. شماره 54.
8. ساویزی، بهناز (1395). «آموزش ریاضی دبستان با رویکرد آموزش ریاضی واقعیتمدار». مجله رشد آموزش ابتدایی. دوره 19. شماره 8.
9. غلام آزاد. سهیلا (1393). «رد پای آموزش ریاضی واقعیتمدار در ریاضیات مدرسهای در ایران». دوفصلنامه نظریه و عمل برنامه درسی. سال دوم. شماره 3.
10. Freudenthal. H. (1991). Revisiting Mathematics Education. China Lectures Dordrecht: Kluwer Academic Publisher.
11. Panhuizen, M. Van Den. (2001). Realistics Mathematics Educatiom as Work in Progress. In F. L. Lin (Ed), Common Sense in Mathematics Education, 1- 43. Proceedings of 2001 the Netherlands and Taiwan Conference on Mathematics Education, Taipei, Taiwan, 19- 23 November 2001.
12. Stoyanova E, Ellerton N. (1996). A framework for research into students' problem posing in school mathematics. In P. C. Clarkson (Ed). Technology in mathematics education. Melbourne, Australia: Mathematics Education Research Group of Australasia; 518- 525.
13. Treffers, A. (1991). Didactical Background of a Mthematics Program For Primary Education. In Leen Streefland (Ed), Realistics Mathematics Education in Primary Schools. Uterecht: Freudental Institute, Utrecht University.
14. Verschaffel, L. (2002). Taking the modeling perspective seriously at the school level: promises and pitfalls (plenary lecture). In A.D. Cockurn & E. Nardi (Eds.), Proceeding of the 26th Conference of the international group for the psychology of mathematics education, vol. 1 (pp. 64- 80). Norwich, England University of East Anglia.
تصویر 1. مسائل صفحه 174 کتاب ریاضی اول دبستان
1. یک اتوبوس 40 صندلی دارد. 24 نفر مسافر در اتوبوس بودند که به ایستگاه امام خمینی(ره) رسید. 4 نفر از اتوبوس پیاده شدند. اتوبوس چند صندلی دارد؟
2. سعیده یک کتابخانهی 2 طبقه دارد. در طبقهی اول 12 کتاب و در طبقهی دوم 13 کتاب دارد. او 4 کتاب از طبقهی اول برداشت و در طبقهی دوم قرار داد. او روی هم چند کتاب در این کتابخانه دارد؟
3. 2 تاکسی از ابتدای خط شروع به حرکت کردند. در یک تاکسی 4 مسافر و در تاکسی دیگر 3 مسافر نشسته بودند. در بین راه چند نفر دیگر سوار شدند. در انتهای این مسیر چند مسافر از تاکسیها پیاده شدند؟