مقدمه
در مقاله رفیعپور (1399) با عنوان «راهبردهایی برای استفاده از رویکرد آموزش ریاضی واقعیتمدار در کلاس درس» که در شماره 136 مجله رشد آموزش ریاضی چاپ شد، سه راهبرد زیر معرفی شدند.
• راهبرد اول: محیط اطراف خود را با دقت مشاهده کنید.
• راهبرد دوم: در مسائل کتابهای درسی، تغییر کوچکی ایجاد کنید.
• راهبرد سوم: از روشهای متفاوت برای طرح مسئله استفاده کنید.
مقاله حاضر روی راهبرد دوم متمرکز است و در آن تلاش میشود، از طریق بیان مثالهای بیشتر، یک راهنمای عملی برای تدریس آموزش ریاضی واقعیتمدار فراهم شود. قبل از ورود به بحث اصلی، لازم است توضیح داده شود که چرا در این مقاله، به دنبال ایجاد تغییر کوچک در مسائل کتابهای درسی ریاضی مدرسهای هستیم تا آنها را به مسائل واقعیتمدار تبدیل کنیم. پیش از آن لازم است توضیح داده شود که اصولاً چرا مطالعه کتابهای درسی ریاضی مهم هستند.
در نظامهای آموزشی متمرکز، مانند نظام آموزشوپرورش ایران، کتابهای درسی نقش مهمی دارند؛ چرا که یکی از منابع اصلی معلمان در تدریس محسوب میشوند. نتایج حاصل از پرسشنامه معلمان ریاضی نشان میدهد که 68 درصد معلمان ریاضی ایرانی شرکتکننده در «مطالعه تیمز 2003» و 100 درصد معلمان ریاضی ایرانی شرکتکننده در «مطالعه تیمز 2007»، از کتاب درسی برای تدریسشان استفاده میکنند [Mollis, et al, 2008]
در مقدمه کتابهای درسی ریاضی اعلام شده است که کتابهای درسی با توجه به سند برنامه درسی ملی نگاشته شدهاند. برای مثال، بخش سخنی با معلم کتاب درسی ریاضی سوم ابتدایی [داودی، رستگار، عالمیان، 1399] را ببینید. در صفحه 41 از سند برنامه درسی ملی، توانایی بهکارگیری ریاضی در حل مسائل روزمره از اهداف آموزش ریاضی دانسته شده است. این در حالی است که پژوهشهای مبتنی بر تحلیل محتوای کتابهای درسی ریاضی مدرسهای نشان میدهند که مسائل مدلسازی در کتابهای درسی ریاضی غایب هستند [رفیعپور، 1391؛ خانی و رفیعپور، 1394]. اما برای نزدیک شدن به اهداف سند برنامه درسی ملی، میتوان با ایجاد تغییراتی کوچک در متن مسائل کتابهای درسی ریاضی، آنها را باورپذیرتر کرد. در ادامه نحوه ایجاد این تغییرات در مثالهای متفاوت نشان داده خواهد شد.
مسائل ریاضی واقعیتمدار
در این بخش شش مثال بیان شدهاند که همگی براساس ایجاد تغییر کوچک در مسائل کتابهای درسی ریاضی دوره اول متوسطه طراحی شدهاند.
مثال اول (رحل قرآن) : در شکل 1 مسئلهای در مورد رحلهای قرآنی آمده است. این مسئله که در صفحه 45 کتاب ریاضی نهم [امیری و دیگران، 1398 ب] آمده است، در زمینه دنیای واقعی مطرح شده و دانشآموز نوعی ایرانی، با رحل قرآن آشناست. ولی چون فرایند صورتبندی و تفسیر و حتی بهکارگیری ریاضی، توسط خود کتاب انجام گرفته و کار کمی به عهده دانشآموز گذاشته شده است، لذا دانشآموز با مسئله درگیر نمیشود. با ایجاد تغییر کوچکی میتوان این مسئله را به یک مسئله ریاضی واقعیتمدار تبدیل کرد.
صورت سؤال مطابق کتاب درسی: با رحلهای قرآنی حتماً آشنایی دارید. در نمونهای از آنها، دو لایه چوبی آن از وسط یکدیگر گذشتهاند. میخواهیم نشان دهیم که این تکیهگاه در هر وضعیتی که باشد، مطابق شکل، همواره فاصله دو لبه کناری آن در دو طرف با هم برابر است. به زبان ریاضی، یعنی در شکل زیر،

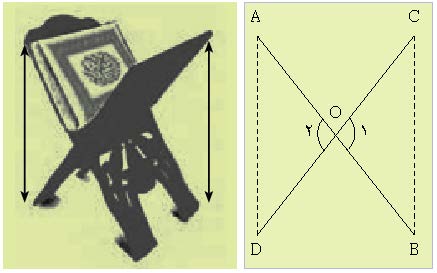
شکل 1. صفحه 45 از کتاب درسی ریاضی پایه نهم
تغییریافته مسئله: علی و محمد دانشآموزان کلاس نهم «مدرسه شهید صدوقی» شهرستان یزد هستند. آنها در ماه مبارک رمضان به مسجد میروند و در برنامه همخوانی دستهجمعی قرآن شرکت میکنند. یک روز بعد از تمام شدن قرآن، علی به محمد گفت: «به نظر تو، تکیهگاه رحل هر جا باشد، فاصله دو لبه کناری آن با هم برابرند؟» محمد پاسخ داد: «بله. تازه میشود دلیل ریاضی هم آورد. نظر شما چیست؟»
مثال دوم (فاصله بین دو روستا): در شکل 2 مسئلهای در مورد راهسازی آمده است. در این مسئله که در صفحه 49 کتاب ریاضی نهم [امیری و دیگران، 1398 ب] آمده است، میتوان از طریق ایجاد تغییر در ظاهر سؤال و استفاده از نامهای آشنا برای دانشآموزان، موقعیت مسئله را باورپذیرتر کرد.
صورت سؤال مطابق کتاب درسی: دو روستای A و B با یک جاده خاکی مستقیم به هم وصل هستند. در آن منطقه یک جاده آسفالته مستقیم ساخته شد که دو روستا در دو طرف آن واقع شدند و جاده آسفالته درست از وسط جاده خاکی عبور میکرد. اداره راهسازی تصمیم گرفته است که از هر روستا، یک جاده آسفالته با کوتاهترین فاصله ممکن تا جاده اصلی بسازد. بنابراین از روستای A یک جاده مستقیم، عمود بر این جاده اصلی و به طول چهار کیلومتر ساخته شد. برای برآورد هزینههای ساخت جاده دیگر از روستای B، مهندسان پیشبینی کردهاند که فاصله روستای B از جاده نیز همین مقدار است؛ یعنی 'AH=BH.
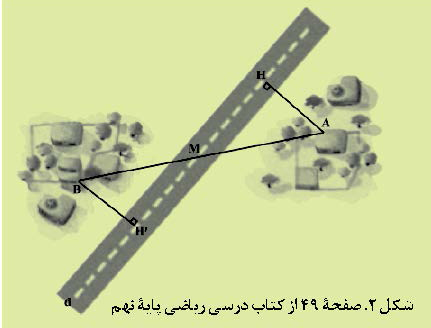
شکل 2. صفحه 49 از کتاب درسی ریاضی پایه نهم
مسئله تغییریافته: روستاهای «حسنآباد» و «محمدآباد» در فاصله 10 کیلومتری از هم قرار دارند. این دو روستا با یک جاده خاکی به هم مرتبط هستند. اداره راه تصمیم گرفته است، آزادراهی بین این دو روستا بگذراند. اهالی این دو روستا هر کدام اعتراض کردند و گفتند: «باید فاصله روستای ما تا این بزرگراه نزدیکتر باشد». اداره راه برای جلوگیری از دعوای این دو روستا تصمیم گرفته است، به گونهای آزادراه را بسازد که فاصله هر دو روستا تا آزادراه احداثی يکسان باشد. لازم به ذکر است، این آزادراه از وسط جاده خاکی بین دو روستا عبور میکند. با توجه به شکل 2، ادعای اداره راه را بررسی کنید.
مثال سوم (نقشهخوانی): در شکل 3، مسئلهای در مورد نقشهخوانی و جهتیابی آمده است. این مسئله که در صفحه 54 کتاب ریاضی نهم [امیری و دیگران، 1398 ب] آمده است، یک فعالیت معتبر در زمینه آموزش ریاضیات واقعیتمدار محسوب میشود، اما دو اشکال اساسی دارد: اشکال اول این است که تصویر درجشده، کیفیت مطلوبی ندارد. اشکال دوم این است که این تصویر برای دانشآموزان غیرتهرانی دور از ذهن است.
صورت سؤال مطابق کتاب درسی:
در شکل 3، نقشه قسمتی از شهر تهران را میبینید. مقیاس نقشه 1 به 100000 است؛ یعنی هر یک سانتیمتر روی نقشه با 100000 سانتیمتر واقعی برابر است. فاصله دو میدان انقلاب و آزادی را پیدا کنید.

شکل 3. صفحه 54 از کتاب درسی ریاضی پایه نهم
به گفته فرودنتال (1991)، شرط آنکه مسئلهای از ارزش انسانی برخوردار باشد، این است که ضمن واقعی بودن، به تجربههای دانشآموزان نزدیک باشد. لذا با توجه به اینکه کتاب درسی ریاضی بهصورت متمرکز چاپ میشود و بومی نیست، معلم میتواند با جایگزین کردن نقشه محل زندگی دانشآموزان، مسئله را واقعیتر کند. به این ترتیب، مسئله برای دانشآموزان ملموستر خواهد شد.
مسئله تغییریافته: معلم میتواند با استفاده از «گوگلمپ»، در شکل 4 نقشه مکان زندگی دانشآموزان را جایگزین نقشه شهر تهران کند. به این ترتیب، مسئله کتاب درسی جرح و تعدیل میشود و برای دانشآموزان غیرتهرانی معنادار خواهد بود. در شکل 4 نقشه قسمتی از شهر یزد آمده است. این نقشه برای دانشآموزان یزدی آشناست و میتوان از دانشآموزان خواست تا فاصله میدان شهید بهشتی تا میدان تاریخی امیرچخماق را محاسبه کنند. البته در این مسئله باید به مقیاس نقشه توجه شود. در شکل 4 مقیاس 1 به 15000 سانتیمتر است.
مثال چهارم (هزینه اشتراک اینترنت): در شکل 5 مسئلهای در مورد هزینه اشتراک اینترنت تلفن همراه آمده است. این مسئله که در صفحه 108 کتاب ریاضی نهم [امیری و دیگران، 1398 ب] آمده است، با تجربه دانشآموزان سازگار است و زمینه واقعی دارد. اما با توجه به اینکه یک راهحل ریاضی مشخص برای حل مسئله وجود دارد، جزو مسائل کاربرد استاندارد1 طبقهبندی میشود.
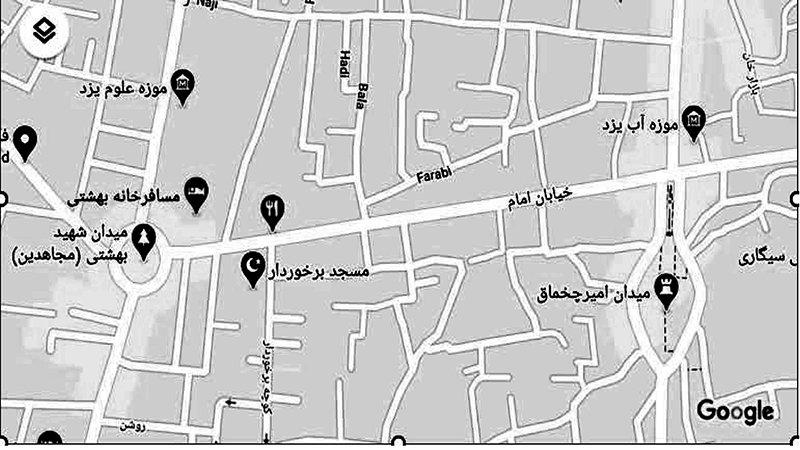
شکل 4. منطقهای از شهر یزد
صورت سؤال مطابق کتاب درسی: هزینه اشتراک یک خط اینترنت روی تلفن همراه 3000 تومان مبلغ ثابت و 2000 تومان برای هر ساعت استفاده است. هزینه کلی x ساعت استفاده از اینترنت را با y نشان دهید و رابطهای بین y و x بنویسید.
یک نوع دیگر از اشتراک اینترنت بدون مبلغ ثابت است؛ ولی برای هر ساعت استفاده، 3000 تومان هزینه دارد. رابطهای بین هزینه اشتراک y و x ساعت استفاده از اینترنت در این حالت بنویسید.
دو خط به معادلههای فوق را در دستگاه مختصات مقابل رسم کنید. محل برخورد این دو خط چه ویژگیای دارد؟ برای 1/5 ساعت استفاده، کدام نوع اشتراک بهتر است؟ بعد از چند ساعت استفاده از اینترنت، اشتراک نوع اول به صرفه خواهد بود؟

شکل 5. صفحه 108 از کتاب درسی ریاضی پایه نهم
تغییریافته مثال چهارم: نوع دیگری از مسائل وجود دارند که در دنیای واقعی مطرح میشوند و از یک بیان غیرریاضی، باید یک مسئله ریاضی صورتبندی شود. این مسائل را «مدلسازی» میگویند. در واقع زمینه واقعیتمدار در این مسائل وجود دارد، ولی برای حل مسئله مدل ریاضی در اختیار دانشآموزان قرار ندارد. برای مثال، در مقاله احمدی و رفیعپور (1393)، یک مسئله مدلسازی با زمینه مرتبط با تلفن همراه، بیان شده است (شکل 6 را ببینید).
مسئله مکالمه با تلفن همراه: نرخ مکالمه با تلفنهای همراه، چه رابطهای با عادتهای مکالمه افراد دارد؟ مجموعه مقرراتی تدوین کنید تا به افراد در انتخاب اپراتور تلفن همراه کمک کند. (مسئله مدلسازی با زمینه مرتبط با تلفن همراه، برگرفته از: احمدی و رفیعپور (1393))
در مسئله مطرحشده در شکل 6، ابتدا باید مجموعه قوانین اپراتورهای تلفن همراه، برای تعیین نرخ مکالمه، بررسی شود. سپس با ساختاربندی و خلاصه کردن قوانین اپراتورهای تلفن همراه، یک مدل ریاضی استخراج خواهد شد. به عبارت دیگر، دانشآموزان برای حل این مسئله به هیچ مدل ریاضی از پیش طراحی شدهای دسترسی ندارد و مدل ریاضی از درون جستار پیرامون مسئله ظهور میکند. اینگونه مسائل (مسائل مدلسازی) از ارزش ریاضی بالایی برخوردار هستند و باعث میشوند، دانشآموز در مورد این سؤال همیشگیشان که ریاضی به چه درد میخورد، تجدیدنظر کنند.
مثال 5 (گردش در جنگل): در شکل 7 مسئلهای از ریاضی نهم [امیری و دیگران،1398 ب] آمده است که در زمینه دنیای واقعی مطرح شده است. اما در حل این مسئله، زمینه هیچ دخالتی ندارد و صرفاً با یک جمع و تقسیم، مسئله حل میشود و دانشآموز بدون درک مفاهیم انرژی و کالری میتواند مسئله را حل کند. به این دسته از مسائل که در زمینه دنیای واقعی مطرح میشوند ولی زمینه مطرحشده نقش خاصی در حل مسئله ندارد، «مسائل مستقل از زمینه»2 میگویند. با ایجاد تغییر کوچکی در مسئله مطرحشده در شکل 7 میتوان یک مسئله مدلسازی به وجود آورد.
دو نفر با وزنهای 85 و 65 کیلوگرم به جنگلی رفتند. آنها در این جنگل به منابع غذایی دسترسی ندارند. برای همین همراه خود مواد غذاییای بردهاند که 4500 کیلو کالری انرژی دارد. اگر فرض کنیم هر انسان روزانه حداقل به اندازه سه برابر وزن خود انرژی نیاز دارد، آنها حداکثر چند روز میتوانند با مواد غذایی خود در جنگل دوام بیاورند؟ (صفحه 94 از کتاب درسی ریاضی پایه نهم)
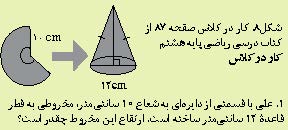
شکل 8. کار در کلاس صفحه 87 از کتاب درسی ریاضی پایه هشتم
تغییریافته مثال پنجم: علی و حسن در تعطیلات عید نوروز به جنگل رفتهاند. آنها 3 کیلوگرم برنج، 300 گرم نمک، 5/1 لیتر روغن و 4 عدد تخممرغ به همراه دارند. اگر آنها روزانه 4500 کیلو کالری انرژی مصرف کنند، محاسبه کنید چند روز میتوانند در جنگل بمانند؟
برای حل این مسئله، دانشآموز ابتدا باید بررسی کند، برنج، نمک، روغن و تخممرغ به چه اندازه کالری انرژی تولید میکنند که معمولاً روی جلد این محصولات نوشته شده است یا میتواند از اینترنت جستوجو کند. سپس بررسی کند که علی و حسن با این مواد چه غذاهایی میتوانند درست کنند و میزان کالری غذای تولیدشده چقدر است. در نهایت هم بگوید چند روز میتوانند در جنگل بمانند. اینکه امکان دارد علی و حسن، با توجه به نوع غذایشان، مسیرهای متفاوتی را طی کنند، یکی از ویژگیهای مسائل زمینهدار در دنیای واقعی است. در این زمینه مسکوویچ (2002) معتقد است که مسائل دنیای واقعی به مسائل بازپاسخ و مسائل با راهحلهای چندگانه مرتبط هستند.
مثال 6 (کلاه جشن تولد): شکل 8 مسئلهای را نشان میدهد که در صفحه 87 از کتاب درسی ریاضی پایه هشتم [امیری و همکاران، 1398 الف] آمده است. با وجود اینکه زمینه این مسئله واقعی است و دانشآموزان با شکل مخروط که شبیه کلاه جشن تولد است، آشنا هستند، ولی بسیاری از آنها در حل این مسئله عملکرد مناسبی ندارند.
تغییریافته مثال ششم: گاهی لازم است شرایطی فراهم شود که دانشآموز راحتتر و بهتر بتواند صورت مسئله را درک کند. در مسئله یافتن ارتفاع مخروط (شکل 8)، اگر معلم از دانشآموزان بخواهد با کاغذ قسمتی از دایره را به شکل سمت چپ تولید کنند و سپس با نزدیک کردن دو سر کمان دایره به یکدیگر، مخروط بسازند، آنگاه دانشآموزان درک بهتری از مسئله خواهند داشت.
سخن پایانی
مثالهای مطرحشده در این مقاله نشان دادند که از طریق ایجاد تغییرات کوچک در متن مسائل کتابهای درسی ریاضی، میتوان آموزش ریاضی واقعیتمدار را در سطح کلاس درس پیاده کرد. پژوهش توکلی و رفیعپور (1398) نشان داد که معلمان ریاضی، برای ترویج آموزش ریاضیات واقعیتمدار، از آمادگی و علاقه کافی برخوردار هستند، اما چون از «نظریه آموزش ریاضیات واقعیتمدار» شناخت کافی ندارند و تنوع و تعداد مسائل زمینهمدار کتابهای درسی محدود است، در این زمینه به موفقیت چندانی دست نیافتهاند. لذا لازم است در آموزشهای پیش از خدمت و ضمن خدمت معلمان ریاضی، مباحثی در مورد نظریه آموزش ریاضی واقعیتمدار گنجانده شود. همچنین لازم است طیف وسیعی از مثالهای زمینهمدار دنیای واقعی توسعه داده شوند و در اختیار معلمان قرار گیرند تا معلمان ریاضی بتوانند براساس نیاز خود و با استفاده از خلاقیتهای فردی، مثالهای مناسب برای کلاس درسشان را تولید کنند.
پینوشتها
1. Standard Application
2. Context-separable problems